Question

In a national survey of 1987 adults, 1570 responded that lack of respect and courtesy in American society is a serious problem, and 1257 indicated that they believe that rudeness is a more serious problem than in past years. Is there convincing evidence that more than three-quarters of U.S. adults believe that rudeness is a worsening problem? Test the relevant hypotheses using a significance level of 0.05. (Round your test statistic to two decimal places and your P-value to four decimal places.)

Answer 1

Answer with explanation:

As per given , we have

`H_0: p\leq(3)/(4)\\\\H_a: p>(3)/(4)`

Since , alternative hypothesis is right tailed, so the test is a right tailed test.

n= 1987

Proportion of adults believe that rudeness is a worsening problem :
`p=(1257)/(1987)\approx 0.6326`

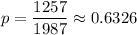
Test statistic :
`z=\frac{\hat{p}-p}{\sqrt{(p(1-p))/(n)}}`

`z=\frac{ 0.6326-0.75}{\sqrt{(0.75(1-0.75))/(1987)}}=-12.09`

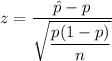
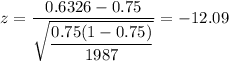
(since , the normal curve takes values of z from -7 to 7, so we use critical value to draw conclusion.)

The critical value for a significance level of 0.005= 1.645

Since , absolute test statistic value (12.09) is greater than the critical value (1.645), it means there is statistical significance and so we reject the null hypothesis.