Question

our buses carrying 140 high school students arrive to Montreal. The buses carry, respectively, 31, 43, 27, and 39 students. One of the studetns is randomly selected. Let X denote the number of students that were on the bus carrying this randomly selected student. One of the 4 bus drivers is also randomly selected. Let Y denote the number of students on his bus. Compute the expectations and variances of X and Y:

Answer 1

V(X)= 39.10

V(Y)= 40

Explanation:

Given that

Total number of student = 140

Bus A - 31

Bus B- 43

Bus C- 27

Bus D- 39

The probability that a student was on the bus is proportional to the number of student. Eg 31/140 in bus A, 43/140 on bus B, ...

E(X) = (31*31/140) + (43*43/140) + (27*27/140) + (39*39/140)

= 35.5

`Var(X) =(31-35.5)^2 * (31)/(140)+(43-35.5)^2 * (43)/(140)+(39-35.5)^2 * (39)/(140)+(27-35.5)^2 * (27)/(140)`

V(X)= 39.10

The bus driver have 1/4 probability on being on any of the buses.

E(Y) = 140/4 = 35

`Var(Y)=((35-31)^2+(35-43)^2+(35-27)^2+(35-39)^2)/(4)`

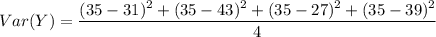
V(Y)= 40