Question

The mean quantitative score on a standardized test for female​ college-bound high school seniors was 350. The scores are approximately Normally distributed with a population standard deviation of 75. A scholarship committee wants to give awards to​ college-bound women who score at the 96th percentile or above on the test. What score does an applicant​ need? Complete parts​ (a) through​ (g) below.

Answer 1

The applicant need a score of at least 481.25.

Explanation:

Problems of normally distributed samples can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by

`Z = (X - \mu)/(\sigma)`

After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the percentile of this measure.

In this problem, we have that:

The mean quantitative score on a standardized test for female​ college-bound high school seniors was 350. The scores are approximately Normally distributed with a population standard deviation of 75. This means that
`\mu = 350, \sigma = 75`.

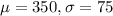A scholarship committee wants to give awards to​ college-bound women who score at the 96th percentile or above on the test. What score does an applicant​ need?

This score is the value of X when Z has a pvalue of 0.96.

Looking at the z score table, we find that Z has a pvalue of 0.96 at
`Z = 1.75`. So

`Z = (X - \mu)/(\sigma)`

`1.75 = (X - 350)/(75)`

`X - 350 = 75*1.75`

`X = 481.25`

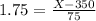
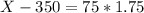
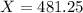
The applicant need a score of at least 481.25.