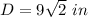Question

A square has a perimeter of 36 inches. Find the length of the diagonal in simplest radical form.

Answer 1

`D=9√(2)\ in`

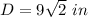
Explanation:

step 1

Find out the length side of the square

we know that

The perimeter pf the square is equal to

`P=4b`

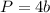
where

b is the length side of the square

we have

`P=36\ in`

so

`36=4b`

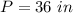
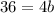
Solve for b

`b=36/4\\b=9\ in`

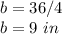
step 2

Find out the length of the diagonal applying the Pythagoras Theorem

Let

D -----> the length of the diagonal of the square

b ----> the length side of the square

we have that

`D^2=b^2+b^2`

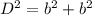
we have

`b=9\ in`

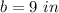
substitute

`D^2=9^2+9^2`

`D^2=2(81)`

`D=√(162)\ in`

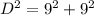
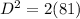
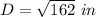
Simplify

`D=9√(2)\ in`