Answer:
Option a) A 95% confidence interval for the mean diameter of the 120 bearings in the sample is
 .
.
Explanation:
We are given the following information in the question:
Sample size, n = 120
Sample mean = 10 mm
Standard Deviation = 0.24 mm
Formula:
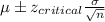
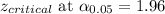

Hence, the correct interpretation for the confidence interval is given by option a).
A 95% confidence interval for the mean diameter of the 120 bearings in the sample is
 .
.
We have to consider the factor of sampling of 120 ball bearings from a population of 10,000 ball bearings.