Answer: e. 16.9<\sigma<29.3
Explanation:
As per given , we have
n= 27 ,
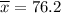 , s=21.4
, s=21.4
Critical value using Chi-square table:-
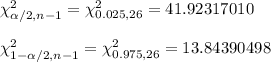
Confidence interval for standard deviation:

Hence, the 95% confidence interval for the standard deviation, σ, of the scores of all subjects :
