Answer:
The required probability is 0.533.
Explanation:
Consider the provided information.
The actual weight of the chocolate has a uniform distribution ranging from 31 to 32.5 ounces.
Let x is the random variable for the actual weight of chocolate.
According to PDF function.

Where
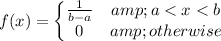
It is given that ranging from 31 to 32.5 ounces.
Substitute a=31 and b=32.5 in above function.

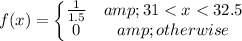
We need to find the probability that a box weighs less than 31.8 ounces
Now according to PDF:
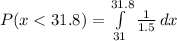
![P(x<31.8)=(1)/(1.5)[31.8-31]\\P(x<31.8)=(0.8)/(1.5)\\P(x<31.8)=0.533](https://img.qammunity.org/2020/formulas/mathematics/college/m6n9t6to139nads47kjg17osldo121tm14.png)
Hence, the required probability is 0.533.