Question

Some Physics questions! Please help!

Answer 1

1) 260 km/h

Let's use the following convention:

positive x-direction = east

positive y-direction = north

Here we have to find the north component of the velocity's airplane, which means we have to find its y-component.

We can use the formula:

`v_y = v sin \theta`

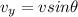
where

v = 750 km/h is the magnitude of the plane's velocity

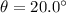`\theta=20.0^(\circ)` is the angle between the direction of the plane and the positive x-axis

Substituting,

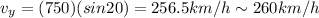
`v_y = (750)(sin 20)=256.5 km/h \sim 260 km/h`

2)
`24^(\circ)` north of east

In order to find the direction of flight, we have to consider that the vector representing the displacement of the plane is the hypothenuse of a right triangle, of which the displacements along the east and north direction are the sides.

Therefore, we have

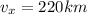`v_x = 220 km` is the displacement towards east

`v_y = 100 km` is the displacement towards north

Therefore, the angle that gives the direction is given by

`tan \theta = (v_y)/(v_x)`

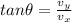
And substituting,

`\theta =tan^(-1)( (100)/(200))=24^(\circ)`

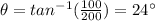
and this angle is measured north of east.