Answer:
a.
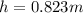
b.
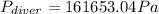
Step-by-step explanation:
Hello,
a.
One could consider the following equation for this exercise's first part:
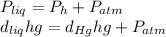
Whereas
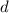 is the density,
is the density,
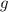 the acceleration of gravity,
the acceleration of gravity,
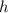 the height and
the height and
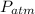 the atmospheric pressure, thus:
the atmospheric pressure, thus:
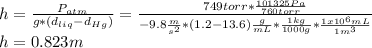
b.
Now, to know the pressure on the diver's body, one uses the following equation considering that the pressure is exerted downwards:
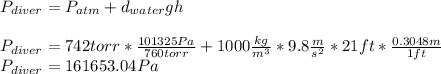
Best regards.