Question

Find two consecutive integers such that 3 times the square of the first is equal to 7 more than 5 times the second

Answer 1

First integer = 3

Second Integer = 4

Explanation:

Let:

First integer = x

Second Integer = x + 1

Now according to given conditions:

3 x^2 = 7 + 5 (x + 1)

3 x^2 = 7 + 5x + 5

3 x^2 = 12 + 5x

Transferring all terms to left side and changing their signs

3 x^2 - 5x - 12 = 0

By quadratic formula:

a = 3

b = -5

c = -12

x =
`((-b)±√(b^2-4ac) )/(2a)`

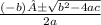
By putting values of a, b and c we get

x = -1 and 3

By ignoring negative integer, take x = 3

Now:

First integer = 3

Second Integer = 4

Proof:

3 x^2 = 7 + 5 (x + 1)

Putting x = 3

3* 3^2 = 7 + 5 (3 + 1)

3* 9 = 7 + 5 (4)

27 = 7 + 20

27 = 27

Hence proved

I hope it will help you!