Answer:
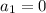 and
and
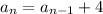
Explanation:
The sequence is given by
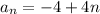 .
.
Now, putting n = 1,
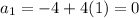 .
.
Now, putting n = 2,
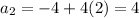
Therefore,
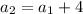 .........(1)
.........(1)
Again, putting n = 3,

Therefore,
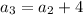 .......... (2)
.......... (2)
Hence, from equations (1) and (2), we can write
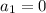 and
and
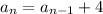
So, this above relation gives the recursive rule for the given sequence. (Answer)