Question

A car rental company has 444cars on their lot. They can rent all 444cars at a rate of $76 per day. They have determined that for every $4 increase in the rental cost, they will rent 3 fewer cars. Find the car rental rate that will maximize revenue for the company.

Answer 1

Car rental rate that maximizes revenue is either $332 or $336 per day

Step-by-step explanation:

The formula for revenue can be stated as:
`R = (76+4x)*(444-3x)`, where x is the amount of $4 increases that are going to be applied.

The first part of the equation
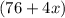`(76+4x)` refers to the car rental rate and the second part of the equation
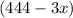`(444-3x)` refers to the cars that are going to be rented.

By elaborating on the formula you have that
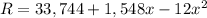`R = 33,744 + 1,548x - 12x^(2)` which can then be simplified into
`R = 2812 + 129x - x^(2)`.

After this, you apply the max value function for a quadratic function:
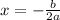`x = -(b)/(2a)`, where we have that b is 129 and a is -1.

Then you get that x must be 64.5. In this situation where it is specified that increases can only increase in $4 amounts, I assume that the x must be rounded. Then your x value for maximum revenue is either 64 or 65.

When you apply x=64 or 65 to the car rental rate function, you have that the rate must be either $332 or $336.