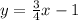Slope intercept form of line passing through (4, 0) and (0, 8) that means slope intercept form of line having x-intercept of 4 and a y-intercept of -3 is
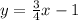 .
.
Solution:
Need to find the equation of a line in slope intercept form
Given that,
x intercept of line is 4 and y intercept of line = -3 ; x intercept is a point where line crosses the x axis.
In our case line have x intercept of 4, which means line crosses x axis at 4. Another catch here is at x axis, value of y is always 0. So we can say that line passes through point (4, 0).
y intercept is a point where line crosses the y axis. In our case line have y intercept of -3 , which means line crosses y axis at -3.Also at y axis, value of x is always 0.
So we can say that line passes through point (0,-3). Now we can say that we need equation of line passing through (4, 0) and (0, -3)
Equation of line passing through point
 is given by
is given by
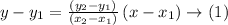
In our case
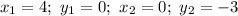
Substituting given value in (1) we get ,
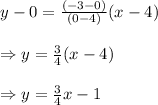
Hence slope intercept form of line passing through (4, 0) and (0, 8) is