Question

A driver traveling at 100 km/hr notices the speed limit changes to 50 km/hr when he is entering town. He takes 0.9 second to slow down to 50 km/hr with constant acceleration. We want to know how many meters the driver travels while slowing down.

50 POINTS TO THE PERSON WHO GETS IT RIGHT FIRST!!!!
HURRRY PLEASE!

Answer 1

B)
`\Delta x = ((v+v_0)/(2))t`

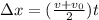
Step-by-step explanation:

In order to find the distance covered by the driver while slowing down, we can use the following suvat equation:

`\Delta x = ((v+v_0)/(2))t`

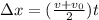
where

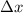`\Delta x` is the distance covered

v is the final velocity

`v_0` is the initial velocity

t is the time

For the car in this problem,

`v_0 = 100 km/h \cdot (1000)/(3600)=27.8 m/s`

`v=50 km/h \cdot (1000)/(3600)=13.9 m/s`

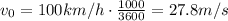
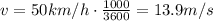
t = 0.9 s

Substituting,

`\Delta x = ((13.9+27.8)/(2))(0.9)=18.8 m`