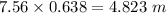Question

A man with a mass of 65.0 kg skis down a frictionless hill that is 5.00 m high. At the bottom of the hill the terrain levels out. As the man reaches the horizontal section, he grabs a 20.0-kg backpack and skis off a 2.00-m-high ledge. At what horizontal distance from the edge of the ledge does the man land (the man starts at rest)?

Answer 1

given,

mass of the man = 65 kg

height = 5 m

mass of the back pack = 20 kg

skis off to 2.00 m high ledge

horizontal distance =

speed of the person before they grab back pack is equal to potential and kinetic energy

`mgh= (1)/(2)mv^2`

`v = √(2gh)`

`v = √(2* 9.8 * 5)`

v = 9.89 m/s

now he perform elastic collision

`v = (m_1v_1)/(m_1+m_2)`

`v = (65* 9.89)/(65+20)`

v = 7.57 m/s

time taken by the skies to fall is

`h = (1)/(2)gt^2`

`t = \sqrt{(2h)/(g)}`

`t = \sqrt{(2* 2)/(9.8)}`

t = 0.6388 s

distance

d = v x t

d = 7.57 x 0.6388

d = 4.84 m

Answer 2

The horizontal distance is 4.823 m

Solution:

As per the question:

Mass of man, m = 65.0 kg

Height of the hill, H = 5.00 m

Mass of the backpack, m' = 20.0 kg

Height of ledge, h = 2 m

Now,

To calculate the horizontal distance from the edge of the ledge:

Making use of the principle of conservation of energy both at the top and bottom of the hill (frictionless), the total mechanical energy will remain conserved.

Now,

`KE_(initial) + PE_(initial) = KE_(final) + PE_(final)`

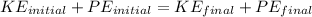
where

KE = Kinetic energy

PE = Potential energy

Initially, the man starts, form rest thus the velocity at start will be zero and hence the initial Kinetic energy will also be zero.

Also, the initial potential energy will be converted into the kinetic energy thus the final potential energy will be zero.

Therefore,

`0 + mgH = (1)/(2)mv^(2) + 0`

`2gH = v^(2)`

`v = √(2* 9.8* 5) = 9.89\ m/s`

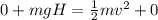
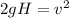
where

v = velocity at the hill's bottom

Now,

Making use of the principle of conservation of momentum in order to calculate the velocity after the inclusion, v' of the backpack:

`mv = (m + m')v'`

`65.0* 9.89 = (65.0 + 20.0)v'`

`v' = 7.56\ m/s`

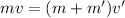
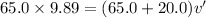
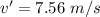
Now, time taken for the fall:

`h = (1)/(2)gt^(2)`

`t = \sqrt{(2h)/(g)}`

`t = \sqrt{(2* 2)/(9.8) = 0.638\ s`

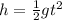
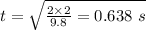
Now, the horizontal distance is given by:

x = v't =
`7.56* 0.638 = 4.823\ m`