Answer:
C. h(x) = f(x + 1)
Please see the graph solution below
Explanation:
1. Take g(x) and replace f(x) into it:

Replacing f(x):
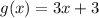
2. To know if one transformation of the function produce the same graph as other function, they must be equal, to find one function equal to f(x) you could use the factorization, that is:
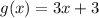
Taking out the number three as the common factor:

3. Take the function f(x) and apply the transformation:
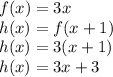
You can see the graphs below and verify that giving values to x the function g(x) and the function h(x) have the same graph.