Question

Two cars move in opposite directions toward each other on a level, straight, one-lane road. When both drivers begin to brake, their front bumpers are 275 meters apart. The smaller car is initially moving at 25.0 m/s and the larger is initially moving at 30.0 m/s. The magnitude of the acceleration of the larger car is 20.0% greater than the magnitude of the acceleration of the smaller. Determine the magnitude of acceleration for each car such that when their front bumpers touch, they have just come to rest.

Answer 1

`a_1=2.5\ m/s^2`

`a_2=3\ m/s^2`

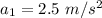
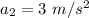
Step-by-step explanation:

t = Time taken

u = Initial velocity

v = Final velocity

s = Displacement

`a_1` = Acceleration of light car

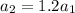`a_2=1.2a_1` = Acceleration of heavy car

`s=ut+(1)/(2)at^2\\\Rightarrow s_1=25* t-(1)/(2)* a_1* t^2\\\Rightarrow s_1=25t-0.5a_1t^2`

`s=ut+(1)/(2)at^2\\\Rightarrow s_2=30* t-(1)/(2)* 1.2a_1* t^2\\\Rightarrow s_2=30t-0.6a_1t^2`

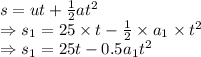
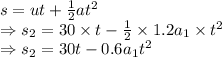
Adding the equations we get

`275=25t+30t-0.5a_1t^2-0.6a_1t^2\\\Rightarrow 275=55t-1.1a_1t^2`

`v=u+at\\\Rightarrow 0=25-a_1* t\\\Rightarrow 0=25-a_1t`

`v=u+at\\\Rightarrow 0=30-1.2a_1* t\\\Rightarrow 0=30-1.2a_1t`

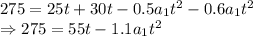
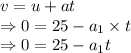
Equating

`25-a_1t=30-1.2a_1t\\\Rightarrow 25-30=(-1.2+1)a_1t\\\Rightarrow a_1t=(-5)/(-0.2)\\\Rightarrow a_1t=25\\\Rightarrow t=(25)/(a_1)`

`\\\Rightarrow 275=55t-1.1a_1t^2\\\Rightarrow 275=55* (25)/(a_1)-1.1a_1 (25^2)/(a_1^2)\\\Rightarrow a_1=(55* 25-1.1* 25^2)/(275)\\\Rightarrow a_1=2.5\ m/s^2`

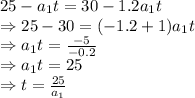
Acceleration of smaller car 2.5 m/s²

`a_2=1.2a_1\\\Rightarrow a_2=1.2* 2.5\\\Rightarrow a_2=3\ m/s^2`

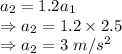
Acceleration of larger car 3 m/s²