Answer:
A.
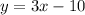
C.
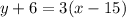
Explanation:
Given:
The given line is

Express this in slope-intercept form
 , where m is the slope and b is the y-intercept.
, where m is the slope and b is the y-intercept.
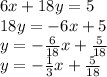
Therefore, the slope of the line is
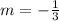 .
.
Now, for perpendicular lines, the product of their slopes is equal to -1.
Let us find the slopes of each lines.
Option A:
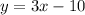
On comparing with the slope-intercept form, we get slope as
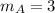 .
.
Now,
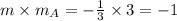 . So, option A is perpendicular to the given line.
. So, option A is perpendicular to the given line.
Option B:
For lines of the form
 , where, a is a constant, the slope is undefined. So, option B is incorrect.
, where, a is a constant, the slope is undefined. So, option B is incorrect.
Option C:
On comparing with the slope-point form, we get slope as
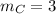 .
.
Now,
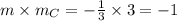 . So, option C is perpendicular to the given line.
. So, option C is perpendicular to the given line.
Option D:

On comparing with the slope-intercept form, we get slope as
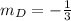 .
.
Now,
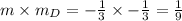 . So, option D is not perpendicular to the given line.
. So, option D is not perpendicular to the given line.