Question

Biologists have studied the running ability of the northern quoll, a marsupial indigenous to Australia. In one set of experiments, they studied the maximum speed that quolls could run around a curved path without slipping. One quoll was running at 3.2 m/s around a curve with a radius of 1.4 m when it started to slip.What was the coefficient of static friction between the quoll's feet and the ground in this trial?

Answer 1

`\mu = 0.746`

Step-by-step explanation:

As we know that the force required to move in circle at uniform speed is known as centripetal force

So here we know that centripetal force is given as

`F = (mv^2)/(R)`

so here the force is due to friction force

so it is given as

`\mu mg = (mv^2)/(R)`

`\mu = (v^2)/(Rg)`

now we have

`\mu = (3.2^2)/(1.4 * 9.8)`

`\mu = 0.746`

Answer 2

`\mu=0.74`

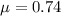
Step-by-step explanation:

It is given that,

Speed of one quoll around a curve, v = 3.2 m/s (maximum speed)

Radius of the curve, r = 1.4 m

On the curve, the centripetal force is balanced by the frictional force such that the coefficient of frictional is given by :

`\mu=(v^2)/(rg)`

`\mu=((3.2\ m/s)^2)/(1.4\ m* 9.8\ m/s^2)`

`\mu=0.74`

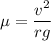
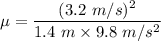
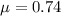
So, the coefficient of static friction between the quoll's feet and the ground in this trial is 0.74. Hence, this is the required solution.