Answer:
2.90 is the pOH of a 0.175 M aqueous solution of
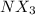 .
.
Step-by-step explanation:
The ionization constant of the base =
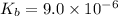
Concentration of the base present initially,c = 0.175 M
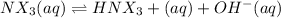
c 0 0
c-x x x
The ionization constant of the base is given by an expression:
![K_b=([HNX_3][OH^-])/([NX_3])](https://img.qammunity.org/2020/formulas/chemistry/college/iv5yzxibnm0vmfi8emv1oi05jxlmaxqo13.png)

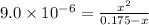
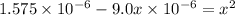
On solving:
x = 0.0012505 M
![[HNX_3]=[OH^-]=0.0012505 M](https://img.qammunity.org/2020/formulas/chemistry/college/hnkf3eqmzpxi2b12su0v3xblivi1z6iekf.png)
![pOH=-\log[OH^-]](https://img.qammunity.org/2020/formulas/chemistry/high-school/n477c3o3xy8p6ug3ipfjqh9fd53hdrrjyq.png)
![pOH=-\log[0.0012505 ]=2.90](https://img.qammunity.org/2020/formulas/chemistry/college/i1z6lqddd06v9lpual2395uv94xgq0rktu.png)
2.90 is the pOH of a 0.175 M aqueous solution of
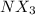 .
.