Question

The graphs of the equations 4x - y = 6 and x + y = 4 intersect at

the point whose coordinates are

Answer 1

The graphs of the equations 4x - y = 6 and x + y = 4 intersect at the point whose coordinates are (2,2)

Explanation:

The graphs of the equations 4x - y = 6 and x + y = 4 intersect at the point whose coordinates are?

We need to find the values of x and y by solving the system of equations.

The values of x and y are the point of intersection of those lines.

We have:

`4x - y = 6--eq(1) \\x + y = 4--eq(2)`

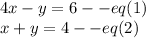
Adding both equations and finding value of x

`4x - y = 6\\ x + y = 4\\-----\\5x+0y=10\\5x=10\\x=(10)/(5)\\x=2`

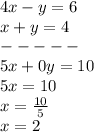
We get, the value of x: x=2

Now, putting value of x in equation 2 to find value of y:

`x+y=4\\Put\:x=2\\2+y=4\\y=4-2\\y=2`

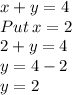
So, we get y=2

Therefore we get x=2 and y=2

The solution set is: (2,2)

So, The graphs of the equations 4x - y = 6 and x + y = 4 intersect at the point whose coordinates are (2,2)