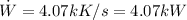Answers:
a)
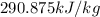
b)
Step-by-step explanation:
a) Since air is considered an ideal gas, its gas constant
 is established in a Thermodynamic table as
is established in a Thermodynamic table as
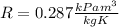 .
.
On the other hand, we have to convert the temperatures from Celsius to Kelvin:

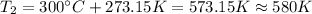
Then, we can find the enthalpy
 from another Thermodynamic table (A-17) with this given temperatures in Kelvin:
from another Thermodynamic table (A-17) with this given temperatures in Kelvin:
For
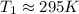 ,
,
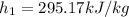 (1)
(1)
For
 ,
,
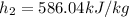 (2)
(2)
Now, the work required by the compressor (the work input)
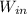 is given by the following equation for
is given by the following equation for
 of air (assuming there is only one inlet and one exit in this system, where the volume is controlled):
of air (assuming there is only one inlet and one exit in this system, where the volume is controlled):
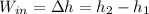 (3)
(3)
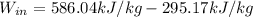
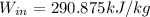 (4) This is the work required by the air compressor
(4) This is the work required by the air compressor
b) The power input
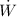 is given by:
is given by:
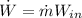 (5)
(5)
Where
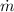 is the mass flow rate at the inlet:
is the mass flow rate at the inlet:
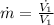 (6)
(6)
We already know the volume flow rate
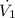 :
:
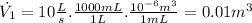 (7)
(7)
The volume at the inlet
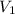 is given by the Ideal gas law equation:
is given by the Ideal gas law equation:
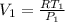 (8)
(8)
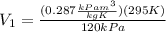 (9)
(9)
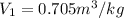 (10)
(10)
Substituting (7) and (10) in (6):
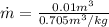 (11)
(11)
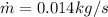 (12)
(12)
Substituting (12) in (5):
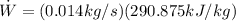 (5)
(5)
Finally: