Answer:

Step-by-step explanation:
If we draw a free body diagram of the sled we will have:

Where:
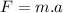 being
being
 the mass of the car and
the mass of the car and
 its acceleration.
its acceleration.
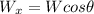 is the horizontal component of the weight of the car
is the horizontal component of the weight of the car
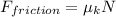 is the friction force where
is the friction force where
 is the normal force
is the normal force
Then:
 (1)
(1)
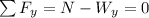
Where
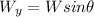 is the vertical component of the weight, then:
is the vertical component of the weight, then:
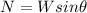 (2)
(2)
Substituting (2) in (1):
 (3)
(3)
Finding
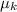 :
:
 (4)
(4)
Simplifying:
