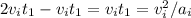Answer:

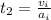
Δd =
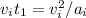
Step-by-step explanation:
As
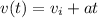 , when the car is making full stop,
, when the car is making full stop,
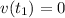 .
.
 . Therefore,
. Therefore,
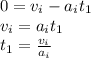
Apply the same formula above, with
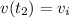 and
and
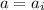 , and the car is starting from 0 speed, we have
, and the car is starting from 0 speed, we have

As
 . After
. After
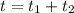 , the car would have traveled a distance of
, the car would have traveled a distance of

Hence
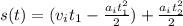
As
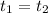 we can simplify
we can simplify
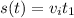
After t time, the train would have traveled a distance of
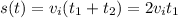
Therefore, Δd would be