Answer:
a) x=63.0
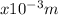 or 6.3cm
or 6.3cm
b) x=116.0
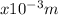 or 11.6cm
or 11.6cm
Step-by-step explanation:
a).
The elastic potential energy is modeling by equation :
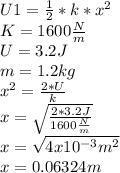
b).
The work energy theorem explain which work is done in this case. the motion began from the rest so K1=K2 equal zero, Ug1 is no yet done and U2is also zero because is the potential energy
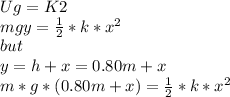
Solving for x
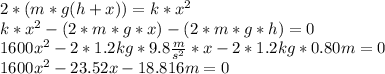
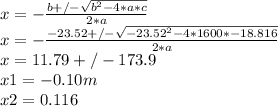
The negative is discard so
x=0.116m