Question

(a) What is the escape speed on a spherical asteroid whose radius is 500 km and whose gravitational acceleration at the surface is 3.0 mlsz? (b) How far from the surface will a particle go if it leaves the asteroid's surface with a radral speed of 1000 m/s? (c) With what speed will an object hit the asteroid if it is dropped from 1000 km above the surface?

Answer 1

(a) 1732.05 m/sec

(b) h = 166.66 km

(c) 2449.48 m/sec

Explanation:

We have given radius of the asteroid R = 500 KM

Acceleration due to gravity at the asteroid
`g=3m/sec^2`

(a) We have to find the escape velocity

We know that escape velocity is given by

`v_e=√(2Rg)=√(2* 500* 10^3* 3)=1732.05m/sec`

(b) We have given initial velocity u = 1000 m/sec

At maximum height velocity will be zero

So final velocity v = 0 m/sec

From third equation of motion

`v^2=u^2+2gh`

`0^2=1000^2-2* 3* h`

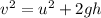
h = 166.66 km

(c) h = 1000 km

We have to find the final velocity

From third equation of motion

`v^2=u^2+2gh`

`V^2=0^2+2* 3* 1000000`

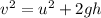
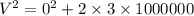
v = 2449.48 m/sec