Question

For this exercise, use the position function s(t) = −4.9t2 + 250, which gives the height (in meters) of an object that has fallen for t seconds from a height of 250 meters. The velocity at time t = a seconds is given by lim t→a s(a) − s(t) a − t . When will the object hit the ground? At what velocity, v, will the object impact the ground?

Answer 1

t=7.14s

v=-69.972 m/s

Step-by-step explanation:

Position function

`s(t)=-4.9*t^(2)+250`

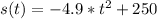
Velocity is the derivative of position function

`V(t)=(dx)/(dt)\\V(t)=-2*4.9*t\\V(t)=-9.8*t`

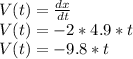
The time the object hit the ground can be find by the given function know that the position is going to be 0m

`s(t)=-4.9*t^(2)+250`

`s(t)=0\\0=-4.9*t^(2) +250\\t=\sqrt{(250)/(4.9)}\\t=7.14s`

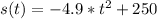
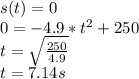
Check:

`s(7.14)=-4.9*(7.14s)^(2)+250\\ s(7.14)=-250+250\\s(7.14)=0m`

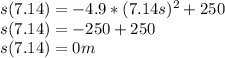
So the velocity can be find using the time discovery before and using the same function but with the derivate

`V(t)=-2*4.9*t\\V(7.14)=-2*4.9*(7.14)\\V(7.14)=-69.972 (m)/(s)`

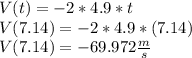
The velocity is negative because the object is moving downward