Question

Solving a word problem using a quadratic equation with rational ..

The area of a rectangle is 45 yd", and the length of the rectangle is 1 yd more than twice the width. Find the dimensions of the rectangle.

Answer 1

The area of a rectangle is 45 yd. The length and width of the given rectangle are 10 and 4.5 yards respectively.

Solution:

The area of the rectangle is given as 45 yard

The relation given to us is the length of the rectangle is 1 yd more than twice the width.

Let length and width be denoted as l and b respectively.

Now as per the given relation we have;

L = 1 + 2b ---- eq 1

We know the area of the rectangle is

Area of rectangle= l × b = 45 --eq 2

From eq 1 and eq 2 we can calculate the dimensions of the rectangle.

`\text { Let } l=(45)/(b) \text { from eq } 1`

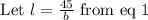
Substituting in eq 2 we get,

`(45)/(b)=1+2 b`

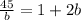
On solving we get,

`2 b^(2)+b-45=0`

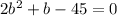
On solving the quadratic equation we get

Width = 4.5 or -5.

Since length cannot be negative, the width of the rectangle is 4.5 yards.

So the length of the rectangle becomes:

l × 4.5 = 45

l = 10

The length and width of the given rectangle are 10 and 4.5 yards respectively.