Question

A 11-mm-diameter plastic sphere whose density is 1150 kg/m3 is dropped into water at 20°C. Determine the terminal velocity of the sphere in water. The density and dynamic viscosity of water at 20°C are rho = 998 kg/m3 and μ = 1.002×10-3 kg/m⋅s, respectively. The drag coefficient for a sphere in laminar flow is CD = 0.5.

Answer 1

0.044 m/s

Step-by-step explanation:

We are given that

Diameter of plastic sphere=11 mm=
`11* 10^(-3)=0.011 m`

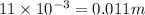
Density of sphere=
`1150 kg/m^3`

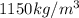
T=
`20^(\circ) C`

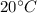
Density of water=
`998 kg/m^3`

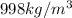
Viscosity of water=
`1.002* 10^(-3) kg/ms`

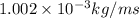
Drag coefficient of a sphere in a laminar flow
`C_D=0.5`

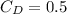
We have to find the terminal velocity of the sphere in water.

Terminal velocity of sphere in water is given by

`V=\sqrt{(4gD((\rho_s)/(\rho_w)-1))/(3C_D)`

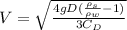
Substitute the values then we get

`V=\sqrt{(4\cdot 9.81* 0.011((1150)/(998)-1))/(3* 0.5)`

`V=0.044 m/s`

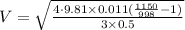
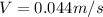
Hence, the terminal velocity of sphere in water=0.044 m/s