Answer:
B.

Explanation:
A quadratic equation is of the form
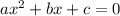 , where, a,b and c are any real numbers and
, where, a,b and c are any real numbers and
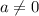 .
.
The quadratic formula is given as:
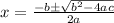
Here, the value of
 can't be 0.
can't be 0.
Now, the necessary condition to check if quadratic formula can be used in the given equations is to check the value of
 after rearranging them in the standard form.
after rearranging them in the standard form.
Let us check each expression for the value of
 .
.
Option A:
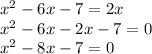
Here,
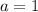 . So, we can use quadratic formula.
. So, we can use quadratic formula.
Option B:
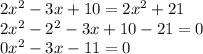
Here,
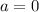 . So, we can't use quadratic formula.
. So, we can't use quadratic formula.
Option C:
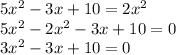
Here,
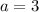 . So, we can use quadratic formula.
. So, we can use quadratic formula.
Option D:
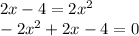
Here,
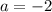 . So, we can use quadratic formula.
. So, we can use quadratic formula.
So, only option B has
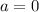 . So, we can't use quadratic formula for option B.
. So, we can't use quadratic formula for option B.