Question

The ages of a sample of fans at a rock concert are listed. 24, 27, 19, 21, 18, 23, 21, 20, 19, 33, 30, 29, 21, 18, 24, 26, 38, 19, 35, 34, 33, 30, 21, 27, 30 1. Order the data entries. 2. Find the median, the rst quartile and third quartile. 3. Calculate interquartile range and interquartile ratio. 4. Draw a relative frequency histogram with seven classes.

Answer 1

1. {18, 18 , 19 , 19 , 19 , 20 , 21 , 21 , 21 , 21 , 23 , 24 , 24 , 26 , 27 , 27 , 29 , 30 , 30 , 30 , 33 , 33, 34 , 35 , 38 }

2a) md= 24 b) Q1=20.5 c) Q3= 30 3) Q3-Q1 =9.5 b) 19/48

Step-by-step explanation:

To answer this question the 1st and the 2nd we need to order the data entries. So from ordering from the lowest to the highest value:

1. {18, 18 , 19 , 19 , 19 , 20 , 21 , 21 , 21 , 21 , 23 , 24 , 24 , 26 , 27 , 27 , 29 , 30 , 30 , 30 , 33 , 33, 34 , 35 , 38 }

2. There are 25 entries.

{18, 18 , 19 , 19 , 19 , 20 , 21 , 21 , 21 , 21 , 23 , 24 , 24 , 26 , 27 , 27 , 29 , 30 , 30 , 30 , 33 , 33, 34 , 35 , 38 }

In odd quantities of observations, the Median equally separates it two parts.

md=24

b) To find out the 1st quartile, we can use this way:

`Q_(1)=(i)/(4)(n+1)\\ Q_(1)=(1)/(4)(25+1)\\ Q_(1)=(1)/(4)(26)=6.5`

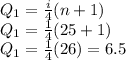
Then 6.5 is between the 6th and 7th position. Let's find the mean of them, now:

`Q_1=(20+21)/(2)= 20.5`

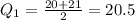
c) Similarly toThe Third Quartile or Upper Quartile

`Q_(3)=(i)/(4)(n+1)\\ Q_(3)=(3)/(4)(25+1)\\ Q_(1)=(3)/(4)(26)=19.5`

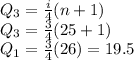
The 19th position and 20th position average is:
`(30+30)/(2) =30`

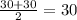
3)

a) To find the Interquartile Range, we just need to find out the difference of the upper quartile and the lower one:
`[tex](Q_3-Q_1)`Q_3-Q_1[/tex]

(30-20.5)=9.5

b) Interquartile Ratio is given by the quotient of the Interquartile Range over the Median

`(IQR)/(md)=(9.5)/(24)=(19)/(48)`

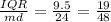
4) Since the Relative frequency Histogram asked is a one with 7 classes. Let's calculate how many values.

k=1+3.32logn

7=1+3.32logn

6=3.32logn

n≈66

Each class must have an interval of 10 ages, for (91-18)/7≈ 10. Notice the orange line intercepts the midpoint of each interval.