Question

Solve the following equation:
|2x - 3|= 4x - 1

Answer 1

Answer: x=2/3

Explanation:

|2x - 3|= 4x - 1

2x-3=4x-1

2x=4x+2

-2x=2

x=-1

4(-1)-1=

-4-1=-5 ==> Absolutes values can't equal a negative number

-(2x-3)=4x-1

-2x+3=4x-1

3=6x-1

6x=4

x=4/6

x=2/3

Answer 2

Hi there,

Happy to help! So let's get into it!

`|2x - 3| = 4x - 1\\`

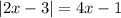
The first step to take is to solve for the Absolute Value.

Thus, we know either
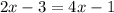`2x - 3 =4x-1` or
`2x-3=-(4x-1)`

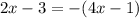
So now let's solve both possibilities:

Possibility #1

`2x - 3 = 4x \\`

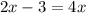
Subtract
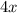`4x` from both sides

`2x - 3 -4x=4x-1-4x`

`-2x -3=-1\\-2x=-1+3\\-2x=2\\x = (2)/(-2) \\x = -1`

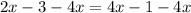
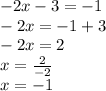
Now let's solve the second possibility

Possibility #2

`2x -3=-(4x-1)\\`

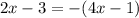
So basically here we need to simplify it. And we can start doing that by adding
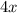`4x` to both sides

`2x - 3 + 4x = -4x +1+4x \\6x - 3 = 1\\6x = 1+3\\6x = 4 \\x = (4)/(6) \\x = (2)/(3)`

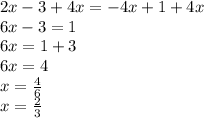
The answer is
`x = (2)/(3)`

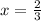
All the best this semester!