Answer:
0.582 g
Step-by-step explanation:
The vapor pressure of the water = 32 torr
The conversion of P(torr) to P(atm) is shown below:
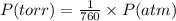
So,
Pressure = 32 / 760 atm = 0.0421 atm
Total pressure = 1.018 atm
Pressure of hydrogen gas = 1.018 - 0.0421 atm = 0.9759 atm
Temperature = 30 °C
The conversion of T( °C) to T(K) is shown below:
T(K) = T( °C) + 273.15
So,
T₁ = (30 + 273.15) K = 303.15 K
Volume = 226 mL = 0.226 L
Using ideal gas equation as:
PV=nRT
where,
P is the pressure
V is the volume
n is the number of moles
T is the temperature
R is Gas constant having value = 0.0821 L.atm/K.mol
Applying the equation as:
0.9759 atm × 0.226 L = n × 0.0821 L.atm/K.mol × 303.15 K
⇒n = 0.0089 moles
According to the given reaction,

1 mole of hydrogen gas is produced from 1 mole of Zn
0.0089 mole of hydrogen gas is produced from 0.0089 mole of Zn
Thus, Moles of zinc = 0.0089 moles
Molar mass of zinc = 65.39 g/mol
Mass= Moles * Molar mass = 0.0089 * 65.39 g = 0.582 g