Question

PLEASE!!!!!!!The adjoining figure shows two circles with the same center. The

radius of the larger circle is 10 cm and the radius of the smaller circle

is 4 cm. Find the area of the shaded region.​

Answer 1

`\boxed{\boxed{\pink{\sf \leadsto Hence \ the \ area \ of \ shaded \ region \ is 264 cm^2}}}`

Explanation:

Here , two circles are given which are concentric. The radius of larger circle is 10cm and that of smaller circle is 4cm . And we need to find thelarea of shaded region.

From the figure it's clear that the area of shaded region will be the difference of areas of two circles.

Let the,

• Radius of smaller circle be r .
• Radius of smaller circle be r .
• Area of shaded region be
  `\bf Area_(shaded)`

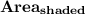
`\bf \implies Area_(Shaded)= Area_(bigger)-Area_(smaller) \\\\\bf\implies Area_(Shaded) = \pi R^2 - \pi r^2 \\\\\bf\implies Area_(shaded) = \pi ( R^2-r^2) \\\\\bf\implies Area_(shaded) = \pi [ (10cm)^2 - (4cm)^2] \\\\\bf\implies Area_(shaded) = \pi [ 100cm^2-16cm^2] \\\\\bf\implies Area_(shaded) = \pi * 84cm^2 \\\\\bf\implies Area_(shaded) = (22)/(7)* 84cm^2 \\\\\bf\implies \boxed{\red{\bf Area_(shaded) = 264 cm^2 }}`

Hence the area of the shaded region is 264 cm².