Question

Two newly discovered planets follow circular orbits around a star in a distant part of the galaxy. The orbital speeds of the planets are determined to be 45.6 km/s and 55.1 km/s. The slower planet's orbital period is 8.68 years. (a) What is the mass of the star? (b) What is the orbital period of the faster planet, in years?

Answer 1

`6.19744* 10^(31)\ kg`

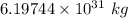
4.91 years

Step-by-step explanation:

G = Gravitational constant = 6.67 × 10⁻¹¹ m³/kgs²

M = Mass of star

v = Oribital velocity of star

T = Oribital time period

R = Radius of orbit

`M=(4\pi^2R^3)/(GT)`

`v=(2\pi r)/(T)\\\Rightarrow R=(vT)/(2\pi)`

`\\\Rightarrow M=(4\pi^2\left((vT)/(2\pi)\right)^3)/(GT)\\\Rightarrow M=(Tv^3)/(2\pi G)`

`\\\Rightarrow M=(8.68* 365.25* 24* 3600* 45600^3)/(2\pi 6.67* 10^(-11))\\\Rightarrow M=6.19744* 10^(31)\ kg`

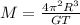
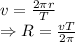
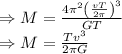
Mass of the star is
`6.19744* 10^(31)\ kg`

`M=(T_1v_1^3)/(2\pi G)=(T_2v_2^3)/(2\pi G)\\\Rightarrow M=T_2v_2^3`

`\\\Rightarrow T_2=T_1\left((v_1)/(v_2)\right)^3\\\Rightarrow T_2=8.68\left((45.6)/(55.1)\right)^3\\\Rightarrow T_2=4.91\ years`

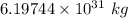
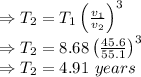
Orbital period of the faster planet is 4.91 years