Question

A card is drawn from a deck of cards numbered one through twenty. The card is NOT replaced and another card is drawn. Find the probability of the outcome.

P(two prime numbers are drawn in a row)

A) 16/95
B) 14/95
C) 4/25
D) 5/13

Answer 1

`(14)/(95)`

Explanation:

I got it right on my exercise!

Answer 2

B) P(two prime numbers are drawn in a row) = 14/95

Explanation:

Total cards in the deck = 20

Total prime numbered cards in deck = { 2, 3, 5, 7, 11, 13, 17, 19} = 8 cards

So, Probability of picking two prime cards from deck (without replacing)

= Probability of picking first prime card x Probability of picking second prime card

P( picking first prime card ) =
`\frac{\textrm{Total prime cards in the deck}}{\textrm{Total available cards}}`

=
`(8  )/(20)  = (2)/(5)`

P( picking second prime card ) =
`\frac{\textrm{Total prime cards in the deck}}{\textrm{Total available cards}}`

=
`(7)/(19)`

Hence, the total probability =
`(2)/(5)  * (7)/(19) = (14)/(95)`

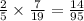
or, B) P(two prime numbers are drawn in a row) = 14/95