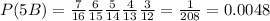Question

Because of a mistake in​ packaging, a case of 16 bottles of wine contained 9 of brand A and 7 of brand​ B, each without labels. All the bottles look alike and have an equal probability of being chosen. Five bottles are randomly selected. ​(a) What is the probability that all five are brand​ A? ​(b) What is the probability that exactly two areare brand​ A? ​(c) What is the probability that none is brand​ A?

Answer 1

a) The probability that all five are brand​ A is 0.0288

b) The probability that exactly two bottles are brand​ A is 0.0288

c) The probability that none of the bottles is brand​ A is 0.0048

Explanation:

We have 9 bottles of brand A and 7 bottles of brand B.

The total of bottles is 16.

a) The probability that all five bottles are brand​ A is given by:

`P(5A)=(9)/(16) (8)/(15)(7)/(14)  (6)/(13) (5)/(12)=(3)/(104)=0.0288`

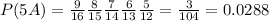
b) Since we have 9 bottles of brand A we calculate the probability of picking two brand A bottles and the we calculate the probability of picking 3 brand B bottles:

`P(2A3B)=(9)/(16) (8)/(15)(7)/(14)  (6)/(13) (5)/(12)=(3)/(104)=0.0288`

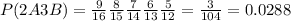
c) The probability that none of the bottles is brand​ A is the same as picking 5 brand B bottles:

`P(5B)=(7)/(16) (6)/(15)(5)/(14)  (4)/(13) (3)/(12)=(1)/(208)=0.0048`