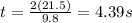Question

A kicker on a sportsball team tries to kick a sportsball so that it stays in the air for a long "hang time." If the ball is kicked with an initial velocity of 24.8 m/s at an angle of 60.0° above the ground, what is the "hang time"?

Answer 1

4.39 s

Step-by-step explanation:

The motion of the ball is a projectile motion, whose time of flight (the time it remains in the air) is given by

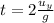`t=2(u_y)/(g)` (1)

where

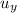`u_y` is the initial vertical velocity of the projectile

`g=9.8 m/s^2` is the acceleration of gravity

The initial vertical velocity of the ball is given by

`u_y = u sin \theta`

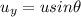
where

u = 24.8 m/s is the initial speed

`\theta=60^(\circ)` is the angle of projection

Substituting,

`u_y = (24.8)(sin 60)=21.5 m/s`

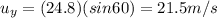
And now by substituting into (1), we find the time of flight (the "hang time"):

`t=(2(21.5))/(9.8)=4.39 s`