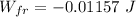Question

A glider of mass 0.240 kg is on a horizontal track, attached to a horizontal spring of force constant 6.00 N/m. There is friction between the track and the glider. Initially the spring (whose other end is fixed) is stretched by 0.100 m and the attached glider is moving at 0.400 m/s in the direction that causes the spring to stretch farther. The glider comes momentarily to rest when the spring is stretched by 0.112 m. How much work does the force of friction do on the glider as the stretch of the spring increases from 0.100 m to 0.112 m?

Answer 1

`W_(fr) = -0.01157\ J`

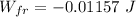
Step-by-step explanation:

given,

mass of glider = 0.24 kg

spring constant = 6 N/m

Initially the spring is stretched by 0.100 m

moving at 0.400 m/s

glider comes to rest when stretched = 0.112

work done by the force of friction = ?

work done by non conservative force

W_{NCF} = E_f -E_i

`W_(fr) = (1)/(2)kx^2-((1)/(2)mv_o^2+(1)/(2)kx_1^2)`

`W_(fr) = (1)/(2)* 6 * 0.112^2-((1)/(2)* 0.24 * 0.4^2+(1)/(2)* 6 * 0.1^2)`

`W_(fr) = -0.01157\ J`

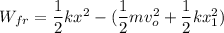
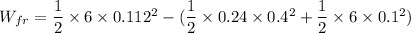
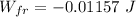
work done by the coefficient of friction
`W_(fr) = -0.01157\ J`