Answer:
For the air:
Final Velocity 160.77m/s
Final Elevation 1,317.43m
the Internal, Kinetic, and Potential Energy changes will be equal.
Step-by-step explanation:
In principle we know the following:
- Internal Energy: is defined as the energy contained within a system (in terms of thermodynamics). It only accounts for any energy changes due to the internal system (thus any outside forces/changes are not accounted for). In S.I. is defined as
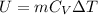 where
where
 is the mass (kg),
is the mass (kg),
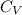 is a specific constant-volume (kJ/kg°C) and
is a specific constant-volume (kJ/kg°C) and
 is the Temperature change in °C.
is the Temperature change in °C.
- Kinetic Energy: denotes the work done on an object (of given mass
 ) so that the object at rest, can accelerate to reach a final velocity. In S.I. is defined as
) so that the object at rest, can accelerate to reach a final velocity. In S.I. is defined as
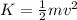 where
where
 is the velocity of the object in (m/s).
is the velocity of the object in (m/s). - Potential Energy: denotes the energy occupied by an object (of given mass
 ) due to its position with respect to another object. In S.I. is defined as
) due to its position with respect to another object. In S.I. is defined as
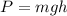 , where
, where
 is the gravity constant equal to
is the gravity constant equal to
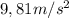 and
and
 is the elevation (meters).
is the elevation (meters).
Note: The Internal energy is unaffected by the Kinetic and Potential Energies.
Given Information:
- Temperature Change 0°C → 18°C ( thus
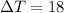 °C )
°C ) - Object velocity we shall call it
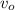 and
and
 , for initial and final, respectively. Here we also know that
, for initial and final, respectively. Here we also know that
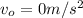
- Object elevation we shall call it
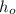 and
and
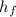 , for initial and final, respectively. Here we also know that
, for initial and final, respectively. Here we also know that

∴ We are trying to find
 and
and
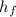 of the air where
of the air where
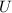 ,
,
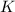 and
and
 are equal.
are equal.
Lets look at the change in Energy for each.
Step 1: Change in Kinetic Energy=Change in Internal Energy
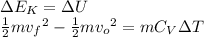
Here we recall that
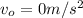 and mass
and mass
 is the same everywhere. Thus we have:
is the same everywhere. Thus we have:
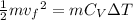
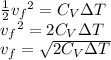 Eqn(1)
Eqn(1)
Step 2: Change in Potential Energy=Change in Internal Energy
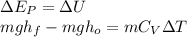
Here we recall that
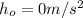 and mass
and mass
 is the same everywhere. Thus we have:
is the same everywhere. Thus we have:
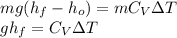
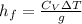 Eqn(2).
Eqn(2).
Finally by plugging the known values in Eqns (1) and (2) we obtain:
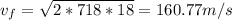
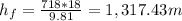
Thus we can conclude that for the air final velocity
 and final elevation
and final elevation
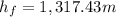 the internal, kinetic, and potential energy changes will be equal.
the internal, kinetic, and potential energy changes will be equal.