Question

A 0.0250-kg bullet is accelerated from rest to a speed of 550 m/s in a 3.00-kg rifle. The pain of the rifles kick is muchworse if you hold the gun loosely a few centimeters from your shoulder rather than holding it tightly against your shoulder.(a) Calculate the recoil velocity of the rifle if it is held loosely away from the shoulder. (b) How much kinetic energy does therifle gain? (c) What is the recoil velocity if the rifle is held tightly against the shoulder. making the effective mass 28.0 kg? (d)How much kinetic energy is transferred to the rifleshoulder combination? The pain is related to the amount of kineticenergy, which is significantly less in this latter situation. (e) Calculate the momentum of a 110-kg football player running at8.00 m/s. Compare the playei’s momentum with the momentum of a hard-thrown 0.410-kg football that has a speed of25.0 m/s. Discuss its relationship to this problem.

Answer 1

(a) -4.6 m/s

We can solve this part by using the law of conservation of momentum: in fact, the total momentum of the bullet-rifle system before and after the shot must be equal.

Before the shot, the total momentum is zero:

p = 0 (1)

After the shot, the total momentum is:

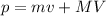`p=mv+MV` (2)

where

m = 0.0250 kg is the mass of the bullet

v = 550 m/s is the velocity of the bullet

M = 3.00 kg is the mass of the rifle

V is the recoil velocity of the rifle

Since momentum is conserved, (1) = (2), so we can solve for V:

`0=mv+MV\\V=-(mv)/(M)=-((0.0250)(550))/(3.00)=-4.6 m/s`

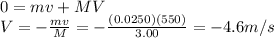
And the negative sign means the rifle will move backward.

(b) 31.7 J

The kinetic energy of an object is given by

`K=(1)/(2)mv^2`

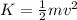
where

m is the mass of the object

v is its speed

The rifle has a mass of

M = 3.00 kg

And a final speed of (speed = magnitude of velocity)

V = 4.6 m/s

Therefore, the kinetic energy it has gained is

`K=(1)/(2)(3.00)(4.6)^2=31.7 J`

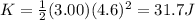
(c) -0.5 m/s

In this case, we just need to repeat the problem as in part (a), applying the law of conservation of momentum:

`0=mv+MV`

where in this case, the mass of the rifle is

M = 28.0 kg

while the other data are unchanged:

m = 0.0250 kg is the mass of the bullet

v = 550 m/s is the velocity of the bullet

Solving for V, we find the new recoil velocity of the rifle:

`V=-(mv)/(M)=-((0.0250)(550))/(28.0)=-0.5 m/s`

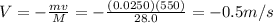
(d) 3.5 J

As in part b), we can apply the equation of the kinetic energy:

The kinetic energy of an object is given by

`K=(1)/(2)mv^2`

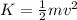
where in this case, we have:

M = 28.0 kg is the mass of the rifle+shoulder

V = 0.5 m/s is the recoil speed of the rifle+shoulder

Substituting into the equation,

`K=(1)/(2)(28.0)(0.5)^2=3.5 J`

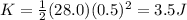
(e) Player's momentum is larger

The momentum of the player is

`p'=MV`

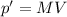
where

M = 110 kg is the mass of the player

V = 8.00 m/s is his velocity

Substituting,

`p'=(110)(8.00)=880 kg m/s`

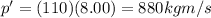
The momentum of the ball is

`p=mv`

where

m = 0.410 kg is the mass of the ball

v = 25.0 m/s is the velocity of the ball

Substituting,

`p=(0.410)(25.0)=10.3 kg m/s`

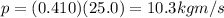
The player's momentum is much larger than the ball's momentum. This problem becomes similar to the previous one in the moment when the player catches the ball: at that point, in fact, the velocity of the player-ball system will change such that their total combined momentum will be equal to the total momentum of the two individual objects before the catch.