Answer:
9 times larger
Step-by-step explanation:
The centripetal acceleration of an object in uniform circular motion is given by
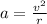
where
v is the speed of the object
r is the radius of the circular path
The car in this problem is moving in a turn, so it is in a circular motion, where r is the radius of the curve. We see that the centripetal acceleration is proportional to the square of the speed,
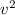 .
.
Let's assume that the initial speed is v = 10 mph, and so the centripetal acceleration is
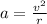
Later, the car's speed increases to 30 mph, which is 3 times the original value:
v' = 3v
So, the new centripetal acceleration is
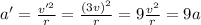
So, 9 times the original acceleration.