Answer:
(a) 8.362 rad/sec
(b) 6.815 m/sec
(c) 9.446
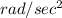
(d) 396.22 revolution
Step-by-step explanation:
We have given that diameter d = 1.63 m
So radius

Angular speed N = 79.9 rev/min
(a) We know that angular speed in radian per sec
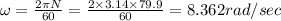
(b) We know that linear speed is given by
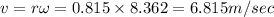
(c) We have given final angular velocity

And
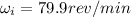
Time t = 63 sec
Angular acceleration is given by
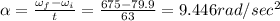
(d) Change in angle is given by
