Question

Two astronauts on opposite ends of a spaceship are comparing lunches. One has an apple, the other has an orange. They decide to trade. Atronaut 1 tosses the 0.125 kg apple toward astronaut 2 with a speed of Vi1=1.13 m/s. The 0.160 kg orange is tossed from astronaut 2 to astronaut 1 with a speed of 1.18 m/s. Unfortunately, the fruits collide, sending the orange off with a speed of 0.999 m/s in the negative Y direction.

A) What are the final speed of the apple in this case (Vf1)?

B) What are the direction of the apple in this case (theta)?

Answer 1

Step-by-step explanation:

Mass of Apple,
`m_a=0.125\ kg`

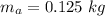
Mass of orange,
`m_o=0.16\ kg`

Initial speed of orange,
`u_o=1.18i`

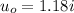
Initial speed of Apple,
`u_a=-1.13i`

Final speed of the orange,
`v_o=-0.999j`

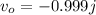
(a) Let
`v_a` is the final sped of the apple. It can be calculated using the law of conservation of momentum as :

`m_au_a+m_ou_o=m_av_a+m_ov_o`

`m_av_a=(m_au_a+m_ou_o)-m_ov_o`

`m_av_a=(0.125* (-1.13i)+0.16* (1.18i))-0.16* (-0.999j)`

`m_av_a=(-0.141i+0.1888i)+0.159j`

`m_av_a=0.0478i+0.159j`

`v_a=(0.0478i+0.159j)/(0.125)`

`v_a=0.382i+1.27j`

`|v_a|=√(0.382^2+1.27^2)=1.32\ m/s`

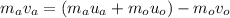
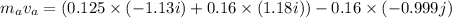
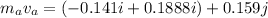
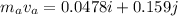
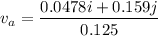
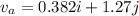
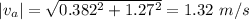
So, the final speed of the apple is 1.32 m/s

(b) The direction of the apple in this case is given by:

`tan\theta=(1.27)/(0.382)`

`\theta=73.25^(\circ)`

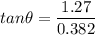
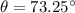
Hence, this is the required solution.