Question

The back of George's property is a creek. George would like to enclose a rectangular area, using the creek as one side and fencing for the other three sides, to create a pasture. If there is 140 feet of fencing available, what is the maximum possible area of the pasture?

Answer 1

The maximum possible area of the pasture = 2450 square feet

Explanation:

Let the length of the creek be 'L'

and, the width of the rectangular area be 'B'

Data provided:

The rectangular area is enclosed using the creek as one side and fencing for the other three sides

Thus, 2B + L = 140 feet

or

L = 140 - 2B .........(1)

Now,

Area of the rectangular land, A = L × B

using (1)

A = ( 140 - 2B) × B

or

A = 140B - 2B²

Now to maximize the area, differentiating the area with respect to width 'B'

we have

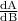`\frac{\textup{dA}}{\textup{dB}}` = 140 - 2 × 2 × B ...........(2)

for point of maxima or minima ,
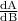`\frac{\textup{dA}}{\textup{dB}}` = 0

thus,

140 - 2 × 2 × B = 0

or

4B = 140

or

B = 35 feet

differentiating (2) with respect to B, for verifying the maxima or minima

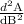`\frac{d^2\textup{A}}{\textup{dB}^2}` = 0 - 2 × 2 = -4

since,
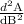`\frac{d^2\textup{A}}{\textup{dB}^2}` is negative,

therefore,

B = 35 feet is point of maxima

from (1)

L = 140 - 2B

or

L = 140 - 2 × 35

or

L = 140 - 70 = 70 feet

Hence,

The maximum possible area of the pasture = L × B

= 70 × 35

= 2450 square feet