Question

One mole of a gas is placed in a closed system with a 20 L vessel initially at T = 300 K. The vessel is then isothermally expanded to 40 L. The gas follows the equation of state: P = RT/V + a/V2 where a = 240 L2 · atm/mol2 and R = 0.08206 L · atm/ mol · K. A. Derive an expression relating (dH/dV)T to measurable properties. B. Find DH for the gas in this process.

Answer 1

Given that

P = RT/V + a/V²

We know that

H= U + PV

For T= Constant (ΔU=0)

ΔH= ΔU +Δ( PV)

ΔH= Δ( PV)

P = RT/V + a/V²

P V= RT + a/V

dH/dV = d(RT + a/V)/dV

dH/dV = - a/V²

So the expression of dH/dV

`(dH)/(dV)=(-a)/(V^2)`

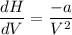
b)

In isothermal process

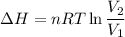`\Delta H=nRT\ln{(V_2)/(V_1)}` (ΔU=0)

Now by putting the all values

`\Delta H=nRT\ln{(V_2)/(V_1)}`

`\Delta H=1* 0.08206* 300\ln{(40)/(20)}`

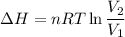
ΔH = 17.06 L.atm