Question

Which of the following would have the same resistance as a copper wire that

is 4 m long and has a cross-sectional area of 0.066 cm??
A. A copper wire that is 8 m long and cross-sectional area of 0.132
cm2
B. A copper wire that is 6 m long and cross-sectional area of 0.022
cm2
C. A copper wire that is 2 m long and cross-sectional area of 0.132
cm2
O D. A copper wire that is 1 m long and cross-sectional area of 0.0złhing
cm2

Answer 1

Answer: your answer is A.

Explanation: just took the a p e x quiz :)

Answer 2

Wire A

Step-by-step explanation:

The resistance of a wire is given by:

`R=(\rho L)/(A)`

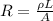
where

`\rho` is the resistivity of the material

L is the length of the wire

A is the cross-sectional area

For wires made of same material,
`\rho` is the same, so we just need to compare the factor
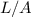`L/A` for the different wires and check which ones have the same ratio.

For the original wire:

`(L)/(A)=(4)/(0.066)=60.6`

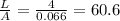
For wire A:

`(L)/(A)=(8)/(0.132)=60.6`

For wire B:

`(L)/(A)=(6)/(0.022)=272.7`

For wire C:

`(L)/(A)=(2)/(0.132)=15.2`

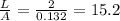
For wire D:

`(L)/(A)=(1)/(0.022)=45.5`

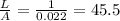
Therefore, the wire that has the same resistance as the original wire is wire A.