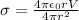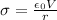Answer:
Part a)
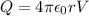
Part b)
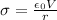
Step-by-step explanation:
Part a)
As we know that potential of the sphere is given as
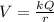
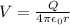
now we have
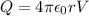
Part b)
Now we know that for conducting charged sphere whole charge is distributed over the surface of the sphere
so we will have
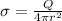
now we have