Answer:
The slope of a line perpendicular to the line whose equation is 4x+6y=108 is

Solution:
Given, line equation is 4x + 6y = 108.
We have to find the slope of the line which is perpendicular to the given line equation.
We know that, product of slopes of perpendicular lines equals to – 1
So, now, let us find the slope of the given line equation.

Now,
slope of given line
 slope of its perpendicular line = -1
slope of its perpendicular line = -1
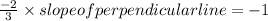
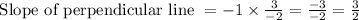
Hence, the slope of the perpendicular line is
