Answer:
The population of a town is 234,876. The population in 5 years is 229062
Solution:
Given, the population of a town is 234,876 and is decreasing at a rate of 0.5% each year.
We have to predict the population in 5 years (round to nearest whole number).
Now, population after 1 year = present population – 0.5% of present population.
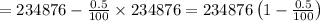
Now, population after 2 years = population after 1 year – 0.5% of population after 1 year.
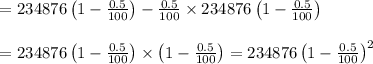
So, population after 5 years will be
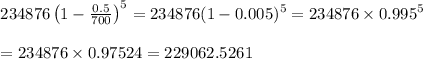
As persons can’t be in fractions, population after 5 years = 229062
Hence, the population of town after 5 years = 229062